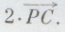Правила сложения векторов, приложенных в точке Р

Правила сложения векторов, приложенных в точке Р 

Чтобы прибавить к вектору

(первое слагаемое) вектор



(вто­рое слагаемое), поступим следую­щим образом (рис. 3): 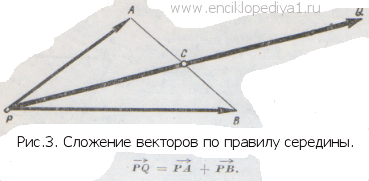а) построим середину С отрезка АВ; б) по­строим точку Q, симметричную точке Р относительно точки С, т. е. так расположенную на луче PC, что точка С является середи­ной отрезка PQ. Полученный век­тор


 

 

 будем называть суммой векторов


(первое слагаемое) и



(второе слагаемое); будем это кратко записывать формулой:


Описанное правило сложения векторов на­зовем правилом середины.

Если слагаемые векторы

и

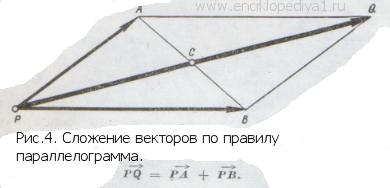
не лежат на одной прямой, то, как легко видеть из

рис. 4, вектор

, являющийся их суммой, представляет собой диагональ параллелограм­ма, сторонами которого являются векторы

 и

Таким образом, для сложения векторов

 и

, не лежащих на одной прямой, можно вместо правила середины воспользоваться сле­дующим правилом: строим параллелограмм PAQB, сторонами которого являются векто­ры-слагаемые

, т. е. из конца А пер­вого слагаемого строим прямую, параллельную второму слагаемому, а из конца B второго слагае­мого строим прямую, параллельную первому сла­гаемому. Точка Q пересечения построенных пря­мых и будет концом вектора PQ, являющегося суммой слагаемых РА и РВ. Для краткости го­ворят: сумма двух векторов есть вектор, являю­щийся диагональю параллелограмма, построен­ного на слагаемых векторах.

то правило сложения векторов называют правилом параллелограмма. Оно, однако, непригодно, когда слагаемые векторы лежат на одной прямой — такие векторы на­зываются коллинеарными; в этом случае применяют правило середины.

Рассмотрим, например, случай, когда век­тор

складывается с самим собой, т. е. когда разыскивается сумма

(рис. 4а). Прибегнем к правилу середины: а) середина отрезка СС, соединяющего концы слагаемых векторов, есть, очевидно, точка С; б) остается построить точку Q, симметричную точке Р относительно точки С,— она будет концом отрезка PQ, серединой которого является точ­ка С.

Таким образом, вектор

большую, чем длина вектора

Этот вектор — сумму двух одинаковых слагаемых — обозна­чают

Итак:


Полезно запомнить (это нам понадобится в дальнейшем), что если точка Q симметрична точке Р относительно точки С, то


Эту формулу записывают также и в следующем виде:


 

 Возвратимся теперь к случаю, когда складываются два произвольных коллинеарных вектора (сонаправленных или противона­правленных). Применяя правило середины, придем к следующим результатам: при сложе­нии двух сонаправленных векторов¹



и

 

 

(рис. 4б) получается вектор

, который имеет такое же направление, как и слагаемые векторы, а его длина равна сумме длин слагаемых векторов; при сложении двух противо­направленных векторов²

и
 

 

 

(рис. 4в) получается вектор, имеющий направление та­кое же, как и направление того слагаемого вектора, который имеет большую длину; его длина равна разности длин слагаемых векторов.

 

¹ Т. е. таких, что точки Р, А, В так расположены на одной прямой, что точка Р лежит вне отрезка АВ

² Векторов, у которых точка Р внутри отрезка АВ.

• АЛГЕБРА ВЕКТОРОВ

• АРИФМЕТИКА НАПРАВЛЕННЫХ ОТРЕЗКОВ
• Направленные отрезки — векторы 
• Правила сложения векторов, приложенных в точке Р 
• Равнодействующая сила    
• Особый вектор — вектор нуль 
• Свойства операции сложения векторов 
• Сумма многих векторов