Целые решения неопределенных уравнений степени выше первой

Целые решения неопределенных уравнений степени выше первой

Решение в целых числах неопределенных уравнений степени выше первой с целыми коэф­фициентами — во многих случаях задача более сложная, чем решение в целых числах неопре­деленных уравнений первой степени.

Индийские математики (V—XII вв.) нашли решение в целых числах некоторых уравнений второй степени с двумя неизвестными. Полно­стью задачу нахождения в целых числах неопреде­ленных уравнений второй степени с двумя неиз­вестными решил в 1766 г. французский матема­тик Ж. Лагранж.

Уравнения третьей степени с двумя неизвест­ными до сих пор до конца не исследованы. С некоторыми типами таких уравнений удалось справиться советскому математику Б. Н. Дело­не. Нужно сказать, что даже установить число решений таких уравнений третьей и более вы­соких степеней исключительно трудно.

В начале нашего столетия норвежскому ма­тематику А. Туэ удалось доказать интересную теорему:

Неопределенное уравнение с целыми коэффициентами:

где n — целое число, большее двух, имеет только конечное множество решений (в частности, мо­жет не иметь решений) в целых числах, за исклю­чением случаев, когда левая часть этого урав­нения есть степень однородного двучлена первой степени или трехчлена второй степени.

Еще более трудным является вопрос о реше­нии в целых числах неопределенных уравнений выше первой степени с тремя и более неизвестны­ми. До сих пор неизвестен общий метод решения таких уравнений. Уравнение (1) является про­стейшим из них. Древние греки и даже вавило­няне знали тождество:

Пользуясь таким тождеством, нетрудно находить натуральные решения уравнения (1). Для этой цели нужно в формулах: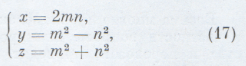

  
 переменным m и n давать натуральные значения с условием, что m>n. При помощи простых сооб­ражений доказывается, что из формул (17) можно получить все решения уравнения (1) в нату­ральных и взаимно простых числах, если па­раметрам m и n давать натуральные, взаимно простые и разной четности значения с услови­ем m>n.

Занимаясь неопределенными уравнениями, известный французский математик П. Ферма высказал в середине XVII в. предположение, что для любого натурального числа n, боль­шего 2, уравнение:

не имеет решений в натуральных числах. До­казательство этого утверждения для n=3 и n=4 было найдено Л, Эйлером.

В дальнейшем предпринимались многочислен­ные попытки доказать это утверждение (так называемую великую теорему Ферма) полностью, но они не имели успеха¹. Однако такие попытки не были безрезультатными — они содействовали возникновению и развитию нового отдела ма­тематики — алгебраической теории чисел.

В 1770 г. шотландский математик Э. Варинг высказал предположение, что для всякого натурального k, не равного 1, существует такое натуральное число r, что при любом натураль­ном N, уравнение:

разрешимо в целых числах. Доказательство част­ного случая этого утверждения принадлежит Ж. Лагранжу. Он установил, что всякое число можно представить в виде суммы четырех квад­ратов целых неотрицательных чисел, например:

Полностью эту теорему удалось доказать в 1909 г. немецкому математику Д. Гильберту. Но ему не удалось дать оценку минимального чис­ла r, для которого уравнение (18) разрешимо в целых неотрицательных числах. Значительный успех в определении g(k) (так обозначают наи­меньшее r, для которого при любом натураль­ном N уравнение (18) разрешимо в целых неот­рицательных числах) стал возможен только после создания советским математиком И. М. Ви­ноградовым особого метода для решения этой и сходных с ней задач.

Сравнительно недавно стали изучаться по­казательные неопределенные уравнения. К этой области принадлежит интересная теорема со­ветского математика А. О. Гельфонда:

Уравнение а^х+b^у=c^z, где а, b и с — целые, каждое из которых не равно ни нулю, ни степени двойки, может иметь не более чем конечное число решений в целых числах х, у и z.

Наиболее трудными являются неопределен­ные уравнения, связанные каким-либо способом с простыми числами. Но и в этой области за по­следние годы наметился успех. Мы не будем останавливаться здесь на этой сложной и увле­кательной проблеме.

¹ В настоящее время теорема доказана для всех n ≤ 10 000.

• ПРОСТЕЙШИЕ НЕОПРЕДЕЛЕННЫЕ УРАВНЕНИЯ
• Пифагоровы треугольники
• Взвешивание груза на чашечных весах
• Раскрой фанеры
• Неопределенные уравнения
• Рациональные и целые решения неопре­деленных уравнений первой степени.Метод рассеивания
• Решение задачи о взвешивании
• Неопределенные системы уравнений первой степени
• Решение задачи о раскрое фанеры
• Целые решения неопределенных уравнений степени выше первой