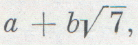Кольца

Кольца

Теперь ясно, когда верна формула

(а+b)²=а²+2ab+b²,

да и все остальные формулы алгебры. Они верны для любых объектов, которые можно склады­вать и умножать, причем выполняются ука­занные выше аксиомы (1). Мы уже знаем три примера объектов, для которых эти аксиомы выполняются. Это — действительные числа, комплексные числа и многочлены.

Математики знают много других примеров множеств с аналогичными свойствами:

1) элементы такого множества можно скла­дывать и умножать, причем сумма и произве­дение двух элементов снова принадлежат тому же множеству;

2) среди элементов множества особо от­мечены два элемента, обозначаемые символами О и 1;

3) для каждого элемента а определен проти­воположный элемент — а, принадлежащий тому же множеству;

4) для сложения и умножения в рассматри­ваемом множестве выполняются все аксиомы (1).

Ввиду того что такие множества часто встре­чаются, для них было введено специальное название — кольцо.

Кроме рассмотренных выше трех примеров, можно указать следующие примеры колец: а) множество всех целых чисел (сумма и произ­ведение целых чисел — целые числа, так же как и число, противоположное целому); б) мно­гочлены с целыми коэффициентами; в) числа вида

А положительные числа (относительно обыч­ных сложения и умножения) кольца не обра­зуют, ведь число, противоположное положи­тельному, уже не является положительным. Позже понятие кольца было расшире­но. Во-первых, отказались от требования, что в кольцо входит элемент 1, для которого a•1=1•a=а. Например, все четные числа (как положительные, так и отрицательные) образуют кольцо без единицы. Нечетные же числа вообще не образуют кольца, так как сумма двух нечетных чисел четна.

Потом отказались и от требования комму­тативности умножения, т. е. отбросили акси­ому аb=bа (сохранив остальные аксиомы). Такие кольца стали называть некоммута­тивными. Примером некоммутативного кольца является кольцо всех кватернионов. Наконец, пожертвовали и аксиомой ассоци­ативности умножения, заменив ее другими ак­сиомами.

Например, стали рассматривать кольца, в которых аксиомы коммутативности и ассоциа­тивности умножения заменяются следующими аксиомами:

аb=-bа                                                     (антикоммутативность);

(ab)c+(bc)a+(са)b=0.

Такие кольца называют алгебрами Ли (по имени норвежского математика С. Ли).

Все это происходило не из любви мате­матиков к обобщениям, а потому, что были найдены важные для практики объекты, для которых имелось естественное сложение и умно­жение, но умножение не было ни коммутатив­ным, ни ассоциативным. Многие такие объекты встретились, например, в современной кванто­вой физике. Разумеется, вследствие введения новых аксиом пришлось заменить многие формулы алгебры новыми. Например, для алгебр Ли вместо формулы (а-b)(а+b)=а²-b² спра­ведлива формула:

(а-b)(а+b)=2ab. Не прав­да ли, удивительно?!

• ЧЕМ ЗАНИМАЕТСЯ АЛГЕБРА

• ЧИСЛА И ДЕЙСТВИЯ
• Необычная конференция
• Фундамент алгебры 
• Сила букв 
• Кольца 
• Поля