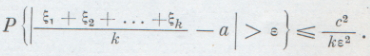Закон больших чисел

Закон больших чисел

Мы ограничимся здесь формулировкой двух теорем, получивших многочисленные теоре­тические и практические применения. Первая из них была доказана Я. Бернулли и опубли­кована в 1713 г.

Производится последовательность незави­симых испытаний, в каждом из которых собы­тие А может произойти с одной и той же ве­роятностью р. Пусть среди первых n испыта­ний событие А наступило в некоторых m. Тогда, как бы мало ни было взято ε>0,

Таким образом, если взять n достаточно большим, то вероятность неравенства

 становится как угодно малой. А так как собы­тия с малой вероятностью имеют мало шансов наступить, то мы видим, что при больших n, как правило, отношение


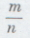будет близко к р.

Теорема Я. Бернулли служит базой для приближенной оценки неизвестных вероятно­стей случайных событий. Длительные наблю­дения над рождениями установили, что в сред­нем на каждую 1000 рождений приходится 511 мальчиков и 489 девочек. Отсюда делается вывод, что вероятность рождения мальчика приблизительно равна 0,511. По вероятности рождения мальчика делаются серьезные про­гнозы о составе населения.

Все страховое дело построено на определе­нии статистическим путем (посредством тео­ремы Бернулли) вероятностей различных собы­тий: смерти лица определенной профессии в те­чение определенного года его жизни, гибели от пожара дома, гибели посевов от града и т. д. На этой базе рассчитываются страховые взно­сы. Эти расчеты оказываются настолько точ­ными, что страховые общества не разоряются, а приносят систематический доход.

Вторая теорема доказана П. Л. Чебышевым в 1867 г. Доказательство Чебышева исключи­тельно просто и изящно. По своим математи­ческим средствам оно вполне доступно уча­щимся девятого класса. Мы ограничимся фор­мулировкой лишь частного случая теоремы.

Предположим, что случайная величина ξ может принимать значения x₁, х₂, ...,х_n соответ­ственно с вероятностями p₁, р₂, ..., р_n( p₁+р₂+...+p_n=1). Средним значением (матема­тическим ожиданием) случайной величины ξ называется сумма Мξ=р₁x₁+p₂x₂+...+p_nx_n.

Представим теперь себе, что имеется по­следовательность независимых случайных ве­личин  ξ₁,ξ₂,...,ξ_k, ..., каждая из которых имеет среднее значение, равное а, и все случайные величины ограничены некоторым числом с. При этих условиях для любого ε>0 имеет место неравенство:

Таким образом, среднее арифметическое не­зависимых случайных величин при большом числе слагаемых становится почти постоянным. Это обстоятельство исключительно важно, оно находит широкое и разнообразное использо­вание на практике. Пусть, для примера, ξ _k есть результат k-го измерения некоторой ве­личины а, лишенного систематической ошибки (например, постоянной ошибки измеритель­ного прибора). Закон больших чисел утверж­дает, что для получения приближенного значе­ния измеряемой величины следует взять сред­нее арифметическое из результатов измерений, и чем измерений больше, тем среднее арифме­тическое будет ближе к измеряемой величине.

В качестве другого примера рассмотрим дав­ление газа на стенку заключающего его сосу­да. Это давление есть результат суммарного воздействия ударов отдельных молекул о стен­ку. Число этих ударов в единицу времени и их сила — дело случая. Таким образом, давление в каждой части поверхности сосуда подвергает­ся случайным колебаниям. Но так как дав­ление складывается из колоссального числа уда­ров отдельных частиц, то среднее арифме­тическое отдельных производимых ими давле­ний, согласно закону больших чисел, практи­чески достоверно является почти постоянной величиной. Отсюда вытекает, что давление газа в нормальных условиях (для не слишком раз­реженных газов) лишь ничтожно мало колеблет­ся около некоторой постоянной величины. Но это утверждение мы знаем из физики под названием закона Паскаля. Таким образом, мы за­кон Паскаля получили не как опытный факт, а как результат теории, как следствие из об­щей теоремы теории вероятностей, из теоремы Чебышева.

Заметим, что теорема Чебышева содержит в себе теорему Бернулли как простейший ча­стный случай, когда все случайные величины могут принимать лишь два значения 0 и 1, соответственно с вероятностями 1-р и р.

• НАУКА О СЛУЧАЙНОМ
• Обыденные представления     
• Примеры случайных событий
• Зачем нужно изучать случайные явления     
• Зарождение науки о случае    
• Теоремы сложения и умножения вероятностей     
• Дополнительные исторические сведения        
• Закон больших чисел                                                        Сколько рыб в озере?
• Некоторые современные направления развития теории вероятностей