ГРУППЫ. Умножение геометрических преобразований

ГРУППЫ. Умножение геометрических преобразований 

О том, что такое геометрические преобра­зования и как они применяются для решения задач, было подробно рассказано в статье «Гео­метрические преобразования». На первый взгляд может показаться, что эта область мате­матики относится целиком к геометрии, а ал­гебраистам там делать нечего. Но это не так; оказывается, геометрические преобразования можно умножать, а ведь алгебра изучает свойства самых различных действий, в том числе и умножения преобразований.

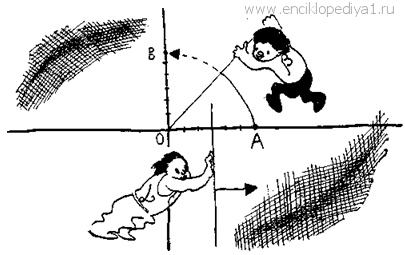
Как же умножить геометрическое преобра­зование α на геометрическое преобразование β? А очень просто — сначала сделать преобразо­вание α , а потомβ . В результате получится новое преобразование. Его называют про­изведением преобразований α и  β и обо­значают αβ„ Пусть, например, α  — поворот плос­кости вокруг точки О на 30°, а  β — поворот вокруг той же точки на 45°. Сделав эти пово­роты один за другим, получим поворот плос­кости вокруг точки О на 75°. Этот поворот и является произведением поворотов α и β .

Умножение преобразований похоже по своим свойствам на умножение чисел. Например, для умножения преобразований верен ассоциативный закон:

α(βγ)=(αβ)γ

(и α (βγ), и (αβ)γ сводятся к последовательному применению преобразований α, β, γ). Есть и преобразование, играющее роль единицы, т. е. такое, что для любого преобразования α  верна формула  α•е=е•α=α. Им является тождественное преобразование е, оставляющее все точки на месте. Ясно, что если сначала сде­лать преобразование е, т. е. оставить все неиз­менным, а потом преобразование  α, то это все равно что сделать только преобразование α . Поэтому е•α =α . Точно так же доказывается, что α•е=α.

— А нужно ли доказывать последнее равен­ство?— спросит читатель. — Ведь уже доказано, что е•α=α, а от перестановки сомножителей произведение не меняется. Вспомните, однако, что при умножении кватернионов пере­ставлять слагаемые нельзя. Оказывается, их нельзя переставлять и при умножении преоб­разований. Вот простой пример.

Пусть α  — сдвиг вдоль оси Ох на 6 единиц, а β —поворот на 90° вокруг точки О. При преобра­зовании α начало координат перейдет в точку А(6; 0). При преобразовании β (т. е. при пово­роте на 90°) точка А перейдет в точку 5(0; 6). Таким образом, преобразование α •β переводит точку О в точку В. Произведем теперь те же преобразования в обратном порядке. При пово­роте α точка О останется на месте. При сдвиге же β точка О перейдет в точку А. Значит, β•α пере­водит О в точку А, а не в точку В. Мы видим, что α•β≠β•α. 

Итак, умножение преобразований не обла­дает свойством коммутативности. Выполнение равенства αβ=βα является для преобразо­ваний не правилом, а исключением. Одно из таких исключений дается формулой: αе=еα.

Преобразования можно не только умножать, но и делить друг на друга. Для чисел деление сводится к умножению на обратное число, на-

пример:

Пусть преобразование а переводит точку Р в точку Q. Тогда обратное ему преобразование α^-1 переводит Q обратно в точку Р. Например, если α — сдвиг вправо на отрезок α , то α^-1 сдвиг влево на тот же отрезок α .

Ясно, что если сначала сделать преоб­разование  α, а потом преобразование α^-1, то в результате все точки вернутся на свои места и получится тождественное преобразо­вание. Поэтому  α•α^-1=е. Точно так же α^-1• α=е.

Теперь ясно, как можно делить преобра­зования. Только, в отличие от чисел, для пре­образований есть два вида деления — сле­ва и справа. Если разделить преобразо­вание α слева на β, то получится β^-1α, если справа — то αβ^-1.

Зачем же нужно умножать преобразования? Чтобы разобраться в этом, разберемся в поня­тии равенства геометрических фигур.

• ГРУППЫ    

• Умножение геометрических преобразований  
• Что такое равные фигуры
• Группы геометрических преобразований     
• Разные геометрии  
• Группы симметрии  
• Задача о раскраске куба 
• Симметрия в природе  
• Группы алгебраических преобразований. Теория Галуа     
• Абстрактная теория групп. Отто Юльевич Шмидт  
• Заключение