|
Меню сайта
|
Три задачи о треугольникеТри задачи о треугольнике1. Произвольная точка Р отражена от середины сторон треугольника A1A2A3, т. е. построены точки: P1 — симметричная точке Р относительно середины стороны А2А3, Р2 — симметричная точке Р относительно середины стороны А3А1, Р3— симметричная точке Р относительно середины стороны А1А2. Что можно сказать об отрезках А1Р1, А2Р2 А3Р3? Ответ подскажет опыт, т. е. тщательно выполненный чертеж. Он покажет, что эти три отрезка пересекаются в одной точке, которая делит каждый из них пополам.
Для доказательства выберем начало радиус-векторов в точке Р и, используя экономные обозначения, обозначим А1, А2, А3 радиус-векторы вершин заданного треугольника (рис. 9 а). (Не советуем эти радиусвекторы проводить на чертеже, достаточно себе их представить.) Тогда, в силу условия задачи, радиус-векторы точек Р1, Р2, P3, отражений точки Р, определяются по формулам: P1=A2,+А3; Р2=А3+А1; Р3=А1+А2. Пусть С1 — середина отрезка A1P1; тогда: 2•С1=А1+Р1=А1+(А2+А3). Пусть С2 — середина отрезка А2Р2, тогда: 2•C2=A2+P2=A2+(A3+А1). Учитывая, что правые части этих формул равны между собой, придем к выводу, что 2•С1=2•С2, т. е. убедимся, что отрезки А1Р1 и А2Р2 имеют общую середину С, имеющую радиус-вектор C1=С2. Аналогичным способом убедимся, что и отрезки A1P1 и А3Р3 имеют общую середину С, имеющую радиус-вектор C1=С3, Таким образом, все три отрезка имеют общую середину С, а это и требовалось доказать. Запомним, что 2•C=A1+A2+A3 (α) 2. Пусть точки Q1, Q2, Q3 — середины отрезков Р2Р3, P3P1, ,P1P2, рассмотренных в предыдущей задаче, а точки М1, М2, М3 — середины сторон А2А3, А3А1, А1А2. Что можно сказать об отрезках M1Q, M2Q2, M3Q3 Из рис. 9 б
2•Q1=Р2+Р3=(А3+А1)+(А1+А2)=2•А1+А2+А3, (β) 2•Q2=P3+Р1=(А1+A2)+(А2+А3)=2•A2+A3+A1, (β') 2•Q3=Р1+Р2=(А2+А3)+(А3+А1)=2•A3+A1+A2, (β'') Если D1 — середина отрезка М1 Q1, то 2•Dl = M1+Q1 и, следовательно, 2•(2D)=(M1+Q1)+(M1+Q1)=2•M1+2•Q1=(А2+А3)+(2•А1+А2+А3)=(А1+А2+А3)+(А1+А2+А3)=2•(А1+А2+А3) (γ) Аналогичным образом получим: 2•(2D2)=(M2+Q2)+(M2+Q2)=А3+А1+(2•А2+А3+А1)=2•(А2+А3+А1) (γ') 2•(2D3)=2•(А3+А1+А2) (γ") Правые части формул (γ), (γ'), (γ") равны между собой, и поэтому D1=D2=D3, что и требовалось доказать. 3. Что можно сказать о прямых A1Q1, A2Q2, A3Q3? Ответ. Они пересекаются в одной точке, которая симметрична точке Р относительно точки С (сделать чертеж). Доказательство. Обозначим буквой Р' точку, симметричную точке Р относительно точки С; тогда Р'=2С и, в силу формулы (α), P'=A1+A2+A3. Обозначим теперь буквой А1' середину отрезка А1Р'; тогда: 2•А'1=А1+Р'=2•А1+А2+А3. Правая часть этой формулы совпадает с правой частью формулы (β), и поэтому А'1=Q1, т. е. точка А'1 есть не что иное, как уже известная нам точка Q1. Отсюда следует, что точка Р' лежит на прямой A1Q1. Аналогичным образом докажем, что она лежит и на прямой A2Q2, и на прямой A3Q3, а это и требовалось доказать.
|
ПОИСК
Block title
|

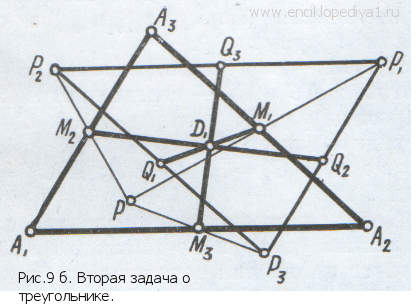 видно, что они пересекаются в одной точке, которая является их общей серединой. Вот алгебраическое доказательство:
видно, что они пересекаются в одной точке, которая является их общей серединой. Вот алгебраическое доказательство: 