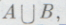|
Меню сайта
Статистика
|
Удивительная алгебра. Д. БульУдивительная алгебра. Д. БульДо сих пор все рассматриваемые законы действий над множествами совпадали с законами действий над числами. Однако на самом деле алгебра множеств вовсе не копирует в точности алгебру чисел; она обладает и многими удивительными свойствами, не имеющими места в обычной алгебре. Мы начнем со второго дистрибутивного закона, получаемого из первого дистрибутивного закона: (А+В)С = АС+ВС заменой сложения умножением и наоборот: АВ+С= (А+С) (В+С). Как уже указывалось, в алгебре чисел этот второй дистрибутивный закон, вообще говоря, места не имеет. По-другому обстоит дело с алгеброй множеств. На рис. 16, а
заштрихованы множества АВ и С, так что заштриховано на этом рисунке множество АВ+С. На рис. 16,б заштрихованы множества A+С и В+С, так что двойной штриховкой покрыто множество (A+С)(В+С). Но легко видеть, что множество, покрытое на рис. 16,б двойной штриховкой, — это в точности то множество, которое заштриховано на рис. 16, а. Таким образом, для любых трех множеств А, В и С: АВ+С= (А+С) (В+С). Далее, выше мы отмечали курьезное равенство: а+1=1, получаемое из равенства а•0=0
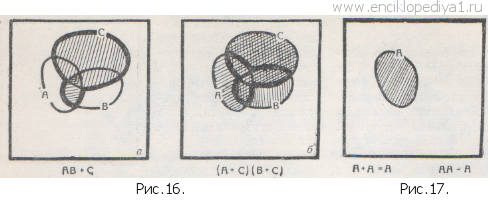
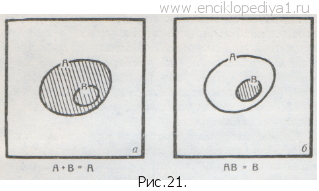
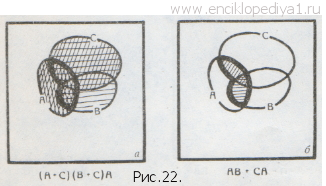
А+I=I. В самом деле, сумма А + I представляет собой множество, получаемое объединением универсального множества I и множества А. Но уже множество I содержит все имеющиеся в нашем распоряжении элементы, так что прибавление к нему множества А ничего изменить не может: сумма А+I — это то же самое универсальное множество I! Отметим еще необычные равенства: А+А=А и АА=А, также выполняющиеся для каждого множества А. В самом деле, сумма А+А представляет собой объединение множества А с самим собой. Но при этом мы придем к тому же самому множеству А (рис. 17). Аналогично этому произведение АА есть пересечение множества А с самим собой, но это пересечение не отличается от множества А (см. тот же рис. 17). Последние два равенства можно еще обобщить. Различные множества можно сравнивать друг с другом. Естественно считать, что множество А «больше» множества В, если все элементы множества В содержатся в множестве А. Это соотношение записывается так: AᑐB или ВᑕА; при этом говорят, что «множество А содержит множество В» или «множество В содержится в множестве А». Так, множество С девочек, сидящих в первом ряду (это множество состоит из школьниц Зои, Кати и Наташи), содержится в множестве В учеников, сидящих в первом ряду: ВᑐС (рис. 18). Графически соотношение АᑐВ изображается тем, что фигура В целиком заключается в фигуре А (рис. 19) или В совпадает с А1. Ясно, что если АᑐВ и ВᑐС, то АᑐС (рис. 20); это утверждение аналогично известному свойству неравенств: если а>b и b>с, то а>с. Нетрудно видеть, что если АᑐВ, то А+В=А; АВ=В (рис. 21 а, б). Так как можно считать, что АᑐА, то отсюда вытекают и два выписанных ранее равенства: А+А=А и АА=А. Мы видим, что правила алгебры множеств во многом отличны от правил алгебры чисел. Поэтому, для того чтобы овладеть этой удивительной алгеброй, приходится не только «доучиваться», но частично и «переучиваться»— отказываться от некоторых привычных представлений, связанных с опытом действий с числами. Вот, например, одно из многих необычных, с точки зрения алгебры чисел, тождеств: (А+С)(В+С)А=АВ+СА (рис. 22, а и б).
Укажем теперь еще одно отличие алгебры множеств от алгебры чисел, которое читатель, возможно, и не отметил. Имея дело с числами, мы можем сравнить между собой любые два числа а и b: всегда одно из них больше другого (или эти числа равны). Для двух множеств А и В, однако, как правило, не будет иметь место ни одно из двух соотношений
и
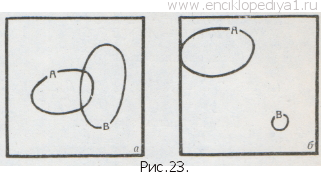
Так, в случае указанных выше множества А отличников и множества В учащихся, сидящих в первом ряду, ни одно из этих множеств нельзя считать большим. Только если одно из двух множеств целиком содержится внутри другого, мы можем указать большее из них; для других же множеств А и В, графически изображенных на рис. 23, а и б, никакое сравнение их невозможно. Таким образом, лишь для некоторых пар множеств А т В можно указать, какое из этих множеств является большим.
Основополагающее сочинение Буля, в котором впервые строилась булева алгебра, называлось «Исследование законов мысли»; оно было напечатано в Лондоне в 1854 г., т. е. более ста лет назад. Название книги Буля сначала может показаться удивительным,— какое отношение имеет курьезная алгебра множеств к законам нашего мышления? На этот вопрос мы постараемся ответить ниже. Поскольку законы действий над множествами отличаются от законов действий над числами, иногда считают, что эти действия нельзя обозначить теми же символами, которые используются в алгебре чисел. В математической литературе сумма множеств А и В часто обозначается через
а произведение этих же множеств через
 При этом правила действий булевой алгебры множеств записываются в следующем виде:
 (коммутативные законы);
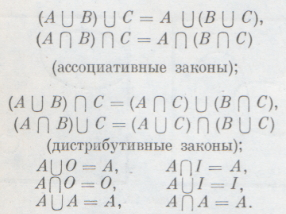
Мы, однако, предпочтем во всех случаях пользоваться знакомыми символами сложения и умножения. 1 Соотношение АᑐВ, строго говоря, переносит в алгебру множеств не соотношение а>b алгебры чисел, а соотношение аіb («число а больше или равно b»).
|
ПОИСК
Block title
|
заменой нуля единицей и умножения сложением. Но курьезным это равенство является лишь в алгебре чисел. В алгебре же множеств, очевидно, для любого множества А: 
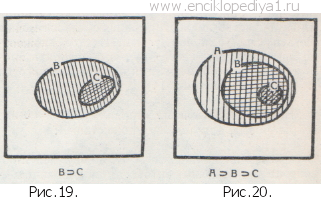
Алгебра множеств с ее своеобразными законами действий, одновременно и напоминающими правила действий над числами, и отличными от этих правил, была впервые указана замечательным английским математиком прошлого века Дж. Булем, отцом известной писательницы Этель Лилиан Войнич (автора романа «Овод»). По имени Буля алгебру множеств часто называют «булевой алгеброй».
