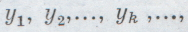Мощность множества

Мощность множества

Нам нужно осмыслить полученный резуль­тат и подвести некоторые итоги всему до сих пор сказанному. Мы начали с понятия взаим­но-однозначного соответствия между двумя множествами, возможность которого (в случае конечных множеств) равносильна тому, что оба множества состоят из одного и того же числа элементов. Это обстоятельство указывает путь и к установлению количественного равенства, или количественной эквивалентно­сти, между двумя бесконечными множест­вами. Мы скажем, что два (конечных или бес­конечных) множества количественно эквива­лентны, или имеют одну и ту же мощность, если между ними возможно установить взаим­но-однозначное соответствие. Понятие «одина­ковой мощности» означает для конечных мно­жеств, что они состоят из одного и того же числа элементов.

Далее скажем, что множество А имеет боль­шую мощность, чем множество В, если можно множество В отобразить взаимно-однозначно на часть множества А и в то же время нельзя отобразить множество А на часть множества В. Теперь можем сказать, что счетные мно­жества — это множества, количественно эквива­лентные множеству натуральных чисел. Но существуют множества и несчетные, например множество всех действительных чисел, интер­вала (0 ; 1) и любого другого интервала¹.

Для того чтобы убедиться в том, что всякое несчетное множество имеет большую мощность, чем каждое счетное множество (все счетные мно­жества имеют, очевидно, одну и ту же мощ­ность), надо доказать следующие два пред­ложения:

1. Всякое подмножество счетного множе­ства или конечно, или счетно.

2. Всякое бесконечное (значит, в частности, всякое несчетное) множество содержит счетное.

Доказательство первого утверждения. Пусть X — счетное множество, Х₀ — какое-нибудь подмножество (т. е. часть) множества X. Элементы множества X могут быть занумерованы посредством натуральных чисел, т. е. записаны в виде:

Среди этих элементов содержатся и все элементы множества Х₀. Пусть это будут — в порядке возрастания номеров в последовательности (2) — элементы:

Возможно одно из двух: или последовательность (3) обрывается на каком-то конечном

шаге k, т. е. множество Х₀ состоит из конеч­ного числа элементов:

или же мы имеем бесконечную последовательность:
которую можем переписать, полагая

в виде:


непосредственно показывающем, что Х₀ — счетное множество.

Доказательство второго ут­верждения. Пусть X — бесконечное мно­жество. Выбираем в X какой-нибудь элемент x₁.

Несомненно, в X имеются элементы, отлич­ные от х₁ (иначе X состояло бы из одного элемента и было бы конечным). Возьмем один из таких элементов и обозначим его через x₂, Элементы х₁ и х₂ не исчерпывают множества X, поэтому существует элемент х₃ множества X, отличный как от х₁, так и от x₂. И так далее. Продолжая этот процесс, получим счет­ное множество: x₁, x₂, x₃,..., x_n,..., содержаще­еся в X.

Итак, на вопрос, поставленный в начале нашего изложения: существуют ли бесконечные множества разных «степеней бесконечности» (т. е. разных мощностей),— мы можем ответить утвердительно: существуют состоящие. из действительных чисел множества двух раз­личных мощностей — множество всех дейст­вительных чисел какого-нибудь интервала, с одной стороны, и любое счетное множества действительных чисел (например, множество положительных рациональных чисел) — с дру­гой. К этому выводу мы пришли, обосновывая количественную оценку бесконечных множеств, при помощи понятия взаимно-однозначного со­ответствия. Однако не следует думать, что взаимно-однозначное соответствие между беско­нечными множествами во всем похоже на взаимно-однозначное соответствие между мно­жествами конечными.

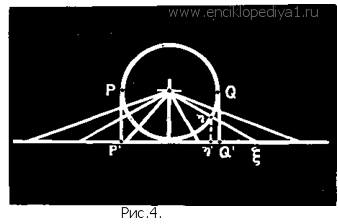
1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...,

2, 4, 6, 8, 10, 12, 14, 16, 18, 20,...,

получим взаимно-однозначное соответствие между множеством всех натуральных чисел и его частью — множеством одних лишь чет­ных чисел.

Другой пример: существует взаимно-одно­значное отображение между множеством всех действительных чисел (между всей числовой прямой) и любым ее интервалом.

Для того чтобы получить такое соответст­вие, можно поступить так. Построим в пло­скости окружность, касающуюся сверху оси абсцисс, и возьмем нижнюю полуокружность PQ этой окружности (рис. 4). Концы Р и Q полуокружности к ней не причисляются. Уста­новим взаимно-однозначное соответствие меж­ду всеми точками полуокружности PQ и всеми точками числовой прямой. Для этого сначала поставим в соответствие каждой точке x пря­мой ту точку h полуокружности, в которой ее пересекает луч, идущий из центра окруж­ности в точку x.

Теперь спроектируем полуокружность PQ на интервал Р'Q' оси абсцисс и поставим в соответствие точке h полуокружности ее проекцию h'.

В результате каждой точке x прямой ока­залась поставленной в соответствие точка h' интервала P'Q', и полученное соответствие есть взаимно-однозначное отображение всей числовой прямой на интервал P'Q'.

Можно доказать и другие, кажущиеся на первый взгляд парадоксальными, теоремы в мощности различных множеств. Упомянем лишь одну из них: существует взаимно-одно­значное соответствие между всеми точками прямой и всеми точками плоскости.

Заметим, наконец, следующее. В матема­тике наибольшее значение имеют так называ­емые числовые множества, т. е. множества, эле­ментами которых являются действительные числа. Все известные в настоящее время чис­ловые множества или счетны, или имеют ту же мощность, что и вся числовая прямая. Воз­никла, таким образом, гипотеза, что всякое несчетное числовое множество имеет ту же мощность, что и вся числовая прямая. Эта гипотеза была высказана еще Кантором и из­вестна под названием континуум-гипотезы. Она не доказана до сих пор, что связано, по-види­мому, с большими трудностями, возникающими при рассмотрении произвольных числовых множеств. Трудности эти получают свое осве­щение в так называемой математической ло­гике, и мы о них здесь, конечно, говорить не можем.

Эта статья имеет своей целью дать лишь начальное представление о некоторых простей­ших понятиях обширной области математики — теории множеств, области, возникшей менее чем сто лет назад.

¹ Всякий интервал числовой прямой может быть взаимно-однозначно отображен на интервал (0; 1) например, подобным растяжением или сжатием).

• МНОЖЕСТВА И ОПЕРАЦИИ
• ПОНЯТИЕ МНОЖЕСТВА 
• Множества конечные и бесконечные 
• Взаимно-однозначное соответствие между двумя множествами 
• Множество всех рациональных чисел счетно 
• Множество всех действительных чисел не счетно. Г. Кантор  Фокус геометрии движения
• Мощность множества                                                   Свойства совершенных чисел