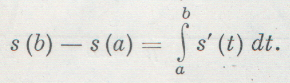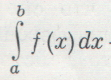|
Меню сайта
|
Формула Ньютона-ЛейбницаФормула Ньютона-ЛейбницаМежду дифференцированием и интегрированием имеется глубокая связь: формула (3) показывает, что путь находится по мгновенной скорости с помощью интегрирования, а формула (9) утверждает, что скорость находится по пути с помощью дифференцирования. Это наводит на мысль, что действия дифференцирования и интегрирования связаны друг с другом примерно так же, как действия сложения и вычитания, умножения и деления, возведения в степень и извлечения корня, т. е. что эти операции взаимно обратны. Например, пользуясь тем, что v(t)=s'(t), можно записать формулу (3) в виде:
Здесь s — путь, пройденный телом начиная с момента t=0. Но может случиться и так, что пройденный путь отсчитывается не с момента t=0, a с какого-то более раннего момента (например, не с момента начала путешествия, а с момента выпуска автомобиля с завода). Тогда путь s придется записать в виде разности s(T)-s(0) пути, пройденного к моменту t=T, и пути, пройденного к моменту t=0. Равенство (3) примет тогда такой вид:
Таким же образом для любых двух моментов времени t=a и t=b справедливо равенство:
Вообще, для любой функции F(x) имеет место равенство:
Эта формула называется формулой Ньютона — Лейбница — в честь знаменитых математиков И. Ньютона и Г. Лейбница, почти одновременно установивших ее в конце XVII в. (примерно через 70 лет после выхода в свет книги И. Кеплера «Новая стереометрия винных бочек»). Следует сказать, что в геометрической форме эту формулу высказал учитель Ньютона И. Барроу в 1670 г. Он указал, что вычисление площадей — действие, обратное проведению касательных.
Значение формулы Ньютона — Лейбница состоит в следующем: если мы знаем какую-нибудь функцию F(x), производная которой равна f(x), т. е. F'(х) =f(х), то легко вычислить интеграл
— он равен разности значений функций F(x) в точках b и а. Каждую функцию F(x), для которой F' (х)=f(х), называют первообразной для функции f(x). Значит, если функция F(x) — первообразная для функции f(x), то f(x) — производная для функции F(x). Таким образом, вычисление интегралов сводится в основном к нахождению первообразных. А нахождение первообразных есть задача, обратная дифференцированию. Поэтому, чем большее число функций мы будем уметь дифференцировать, тем больше первообразных будем знать и тем больше интегралов сможем найти. Пока что мы умеем дифференцировать только многочлены. Этого уже достаточно, чтобы интегрировать любые многочлены (не прибегая к примененным выше геометрическим приемам). Но во многих задачах встречаются функции, отличные от многочленов. Мы научимся сейчас дифференцировать показательную и тригонометрические функции.
|
ПОИСК
Block title
|