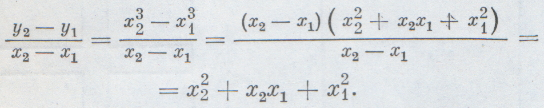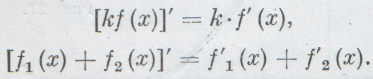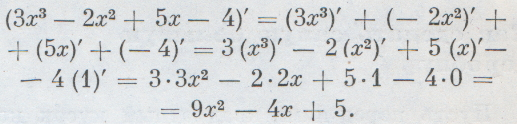|
Меню сайта
|
Производные многочленовПроизводные многочленовИз сказанного выше ясно, что для решения ряда задач физики, геометрии и других наук весьма важно уметь находить производные различных функций (нахождение производных называется дифференцированием). Мы рассмотрим сейчас пример непосредственного вычисления производной. Возьмем функцию у=х3. Отношение, которое нужно рассмотреть при вычислении этой производной, имеет такой вид:
Если теперь х2 будет приближаться к x1, то последнее выражение будет, очевидно, приближаться к значению х21+х21+х21=3x21. Таким образом, производная от функции у=х3 имеет в точке х=х1 значение Зх21, т. е.
(х3)' ?при x=x1=3x21. Более кратко это записывают так: (х3)'=3x2. Предоставляем читателю таким же образом найти производные от функций у=х2 и у=х. Результаты получаются такие:
Эти формулы вычисления производных объединяются, очевидно, одной общей формулой:
Для случая целого положительного значения n эту формулу можно проверить примерно таким же способом, как мы выше вычислили производную от x3. В математике доказывается, что формула (12) верна при любом п. Заметим, что производная единицы (или вообще любой постоянной величины) равна нулю. Это легко следует из формулы (12), а впрочем, ясно и без этого, так как скорость изменения постоянной, очевидно, равна нулю. Заметим теперь, что производная обладает следующими простыми, но важными свойствами: постоянный множитель можно выносить за знак производной; кроме того, производная суммы двух (или нескольких) функций равна сумме производных от слагаемых:
Справедливость этих правил легко проиллюстрировать с помощью формулы (9), примерно так же, как мы сделали выше для интегралов.
Теперь уже легко можно находить производные любых многочленов, например:
Вообще, если
-многочлен n-й степени, то его производная вычисляется по формуле:
|
ПОИСК
Block title
|