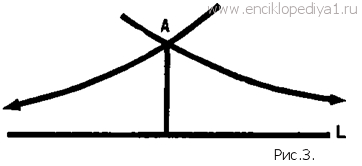
Постулат о параллельных и не евклидовы геометрии

Постулат о параллельных и не евклидовы геометрии

Математики все время испытывали неко­торую неудовлетворенность, связанную с по­стулатом о параллельности, который, как мы видели, формулировался довольно сложно. Ка­залось, что его можно доказать, вывести из других постулатов и аксиом. Начиная с глубо­кой древности и до конца XVIII в. многие геометры пытались доказать этот постулат как теорему.

Однако все доказательства V постулата, которые были придуманы, либо содержали пря­мую ошибку, либо опирались на новое пред­ложение, которого не было среди постулатов и аксиом Евклида. При более тщательном ана­лизе всегда оказывалось, что это новое пред­ложение равносильно постулату о параллель­ности, т. е. из него можно вывести этот постулат и, наоборот, из V постулата можно получить это новое предложение. К началу XIX в. воп­рос о V постулате казался безнадежно запутан­ным. Но как раз в 20-х годах прошлого века было получено совершенно неожиданное реше­ние этого многовекового вопроса. Это решение было связано с совершенно новым взглядом на геометрию, к которому пришли независимо друг от друга три великих геометра: Н. И. Лоба­чевский, К. Ф. Гаусс и Я. Бояи.

Впервые в печати решение вопроса появи­лось в работе Н. И. Лобачевского в 1829 — 1830 гг. (эта работа была доложена Лобачев­ским в Казанском университете еще в 1826 г.), и несколько позже — в 1832 г.— было опубли­ковано исследование Бояи. Гаусс вообще не опубликовал те смелые выводы, к которым пришел.

Новая идея, которая легла в основу решения, состояла в следующем: геометрия Евклида не является единственной возможной геометрией, можно построить и другие системы геометрии, столь же стройные и непротиворечивые, как евкли­дова. При этом и Н. И. Лобачевский, и К. Ф. Гаусс были глубоко убеждены, что новая геометрия получит применение для описания и изучения геометрических свойств нашего пространства.

Такой взгляд противоречил двухтысячелетней традиции, благодаря которой сложилось убеждение, что геометрия Евклида столь же естественна, как смена дня и ночи, и что толь­ко она описывает пространственные соотно­шения между реальными телами.

Как же строить новые геометрические систе­мы? В XVIII в. геометры придумали новый способ доказательства V постулата. Они пред­полагали, что V постулат неверен, и старались прийти к противоречию, как это делается при доказательствах от противного. Действитель­но, если V постулат можно вывести из других постулатов и аксиом геометрии Евклида, т. е. он является теоремой, то предположение, что он неверен, должно было бы привести нас к противоречию. Однако как ни пытались гео­метры получить противоречие, им этого сделать не удавалось. Они получали все новые и новые следствия; некоторые из них выглядели пара­доксально, например: сумма углов треуголь­ника у различных треугольников различна, но всегда меньше 2d; линия, равноотстоящая от некоторой прямой (эквидистанта), сама не яв­ляется прямой; не существует подобных тре­угольников и вообще подобных фигур. Однако ни одно из следствий не противоречило другому следствию и остальным аксиомам евклидо­вой геометрии.

Лобачевский, Гаусс и Бояи пришли к убеж­дению, что противоречия и не получится, по­тому что V постулат не является теоремой в евклидовой геометрии. Что же в таком случае представляют полученные следствия? Оказы­вается — теоремы новой геометрии! Таким обра­зом, для построения новой геометрии нужно было заменить V постулат другим и вывести из новой системы постулатов и аксиом возможные следствия. Они-то и будут теоремами но­вой геометрии.

V постулату Евклида часто придают такую форму: через точку вне прямой в плоскости, определяемой этой точкой и этой прямой, мож­но провести только одну прямую, не пересе­кающую данной.

Если этот постулат не имеет места, то это означает, что:

1) либо можно провести по край­ней мере две прямые, не пересекающие данной (рис. 3),

2) либо таких прямых не существует вовсе (т. е. вообще нет параллельных прямых).

Второе из этих предположений легко при­водится к противоречию с другими аксиомами и постулатами Евклида. Первое же Н. И. Ло­бачевский выбрал в качестве нового постулата о параллельности. Он построил стройную систе­му геометрии, которая носит теперь его имя. При этом Н. И. Лобачевский показал, что гео­метрия Евклида может быть получена как пре­дельный случай новой геометрии.

Исследования Н. И. Лобачевского открыли новую эру в истории геометрии. Если до этого казалось, что в основном в геометрии все сде­лано уже самим Евклидом, то после создания неевклидовой геометрии открылись широкие возможности для новых геометрических изысканий.

В 60-х годах прошлого века немецкий математик Риман предложил новый метод построения всех неевклидовых геометрий, в которых можно мерить длины, площади, углы, объёмы (так называемых метрических геометрий). При этом он не ограничился случаем трехмерного пространства, а строил геометрии пространств любого числа измерений. Интересно отметить, что, в частности, он построил такую геометрию, в которой нет параллельных прямых. Конечно, для построения такой геометрии пришлось отказаться от некоторых других аксиом ев­клидовой геометрии.

Эта геометрия похожа на сферическую, ее называют эллиптической или геометрией Римана (в узком смысле слова, в отличие от общих римановых геометрий). В этой геомет­рии, так же как в геометрии Лобачевского, нет подобных фигур, но сумма углов треугольника в ней всегда больше 2d, а длины прямых линий ограничены.

Были предложены и другие методы построе­ния новых геометрий.

Но в связи с новыми геометриями встали и другие вопросы: геометрия Лобачевского отли­чается от евклидовой постулатом о параллель­ности. Что будет, если заменять и другие по­стулаты? Всегда ли при этом будут получаться новые системы геометрии? В каких случаях новые системы будут непротиворечивыми, т. е. в них нельзя доказать некоторую теорему и одновременно доказать, что эта теорема неверна?

Для ответа на эти вопросы ученые прежде всего вновь обратились к исследованию геомет­рии Евклида с тем, чтобы найти все аксиомы, нужные для ее построения, а затем уже изучить связи между этими аксиомами, посмотреть, что будет, если отбросить одну или несколько из них и заменить другими. Многие математи­ки конца прошлого века занимались этой проблемой, но впервые ее удалось решить немецкому математику Д. Гильберту в 1899 г. В его книге «Основания геометрии» была из­учена первая полная система аксиом геомет­рии Евклида и исследованы вопросы, о кото­рых мы говорили выше. Это направление иссле­дований привело к созданию современного аксиоматического метода, значение которого трудно переоценить.

Неевклидовы геометрии открыли новую эру не только в математике, но и в физике. Как и предвидели создатели этих геометрий, они сде­лались незаменимым математическим аппара­том многих важнейших частей современной физики, особенно теории относительности.

Более подробно о новых геометриях вы можете узнать из статьи «О различных гео­метриях».

Итак, мы видим, что возникновение геомет­рии как науки далеко не закончилось построе­нием системы евклидовой геометрии. Это было только начало, блестящее продолжение которого осуществилось в XIX в.

В настоящее время геометрия представляет большую, широко разветвленную науку, тесно связанную со всеми остальными разделами ма­тематики.

• ФИГУРЫ И ТЕЛА
• Геометрия вокруг нас                                          Поищем числа-,,самородки" 
• Как возникла геометрия                                    Из шести спичек
• Возникновение геометрии как науки            Развлечение с числами
• Построение дедуктивной системы                     Гармония форм
• Постулат о параллельных и не евклидовы геометрии