|
Меню сайта
Статистика
|
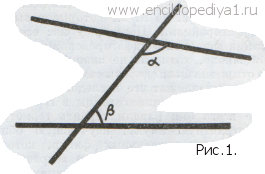
Построение дедуктивной системыПостроение дедуктивной системыВо-первых, ясно, что все правильные предложения доказать нельзя. Действительно, вспомним, как доказываются геометрические предложения. При этом обычно опираются на некоторые другие предложения, которые были доказаны раньше. Эти предложения в свою очередь доказываются ссылками на какие-то третьи теоремы и т. д. Эти ссылки мы могли бы продолжать до бесконечности, и процесс доказательства при этом никогда бы не закончился. Как же быть? Это обстоятельство заметили еще в древности, о нем говорил, например, Аристотель (IV в. до. н. э.). И вот геометры пришли к удивительно смелой мысли, что все геометрические свойства тел нашего пространства можно вывести из небольшого числа основных предложений — аксиом. Эти предложения принимались без доказательств, их справедливость подкреплялась многовековым опытом. Усилия многих геометров были направлены на то, чтобы отыскать все аксиомы, необходимые для построения геометрии. Система, в которой каждое предложение выводится на основании логических правил из конечного числа предложений, принятых без доказательства, и получила название дедуктивной. Первую такую систему геометрии — «Начала» — пытался построить еще в V в. до н. э. Гиппокарт Хиосский. Было еще несколько попыток такого рода, но наиболее совершенная из них знаменитые «Начала» Евклида, которые были написаны около 300 г. до н. э. и служили в течение более 2 тыс. лет образцом математической строгости. Евклид разделил предложения, принятые без доказательства, на аксиомы и постулаты. В качестве постулатов он выбрал предложения, в которых утверждалась возможность выполнения некоторых простейших геометрических построений, например: 1) через две точки всегда можно провести прямую линию, 2) из данной точки данным радиусом можно описать окружность. Как нетрудно видеть, это именно те построения, которые можно сделать с помощью циркуля и линейки. Всякое построение в геометрии Евклида осуществляется с помощью последовательного выполнения простейших построений: проведения прямых, окружностей и отыскания их точек пересечения, поэтому геометрия Евклида есть геометрия циркуля и линейки. Среди постулатов Евклида особое место занимает так называемый V постулат о параллельности. В «Началах» он формулируется так: если две прямые, лежащие в одной плоскости, пересечены третьей и если сумма внутренних односторонних углов меньше 2d, то при продолжении прямые пересекутся с той стороны, где эта сумма меньше 2d (рис. 1). Этот постулат сыграл огромную роль в дальнейшем развитии геометрии, о чем мы будем говорить дальше. Кроме постулатов, Евклид принял также некоторые общие предложения — аксиомы: 1) две величины, порознь равные третьей, равны между собой; 2) если к равным величинам прибавить равные, то и суммы будут равны; 3) целое больше части и др. На основе своих постулатов и аксиом Евклид развил всю планиметрию, а с ее помощью построил элементы алгебры и учение о квадратных уравнениях. В его сочинении содержатся также общая теория отношений, которая применяется в учении о подобии, теория чисел, метод определения площадей и объемов и основы стереометрии. Венчает «Начала» учение о правильных выпуклых многогранниках, т. е. таких, все грани которых являются равными правильными многоугольниками и все многогранные углы при вершинах тоже правильные и равные. Евклид доказал, что существует пять правильных многогранников: тетраэдр, куб, октаэдр, икосаэдр и додекаэдр — и никаких других правильных многогранников не существует (рис. 2). Можно сказать, что в «Началах» Евклида были заложены основы не только геометрии, но и всей античной математики. На новую, более высокую ступень исследования основ геометрии ученые поднялись только в XIX в. Тогда было выяснено, При построении дедуктивной системы геометрии выяснилось, что доказательства служат не только для того, чтобы установить истинность некоторого предложения, но и для выявления взаимосвязей между предложениями. Так, при анализе доказательства предложения о том, что сумма углов треугольника равна 2d, оказалось, что оно зависит от V постулата Евклида, тогда как, например, теорема о том, что внешний угол треугольника больше каждого внутреннего, с ним не смежного, от постулата параллельности не зависит. Таким образом, доказательства помогают уяснить существо, смысл математических предложений. В частности, можно в евклидовой геометрии выделить все те предложения, которые доказываются без постулата параллельности,— они составляют так называемую абсолютную геометрию.
|
ПОИСК
Block title
|
что Евклид перечислил не все аксиомы, которые на самом деле нужны для построения геометрии. В действительности при доказательствах он ими пользовался, хотя и не формулировал их. Однако все это нисколько не умаляет роли Евклида, который первым показал, как можно и как нужно строить математическую теорию. Созданный им дедуктивный метод прочно вошел в математику. В этом смысле все последующие математики, вплоть до наших современников, являются учениками Евклида. 